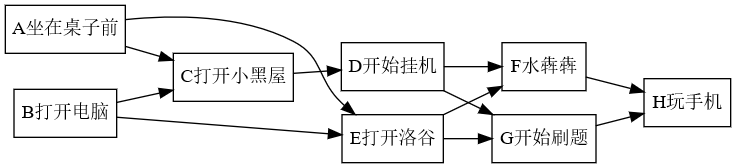
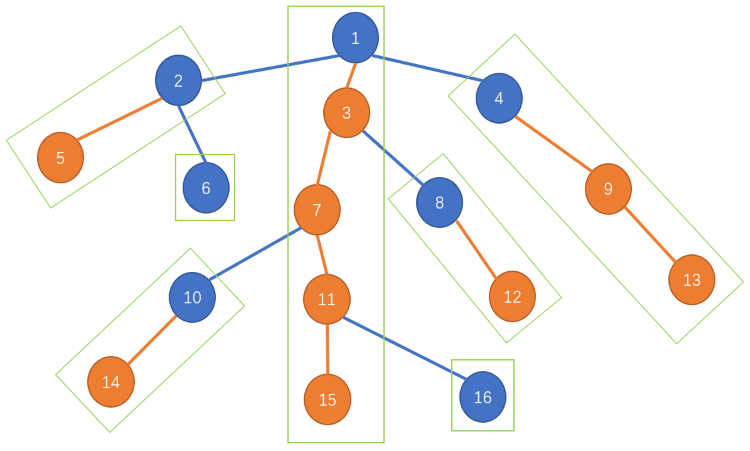
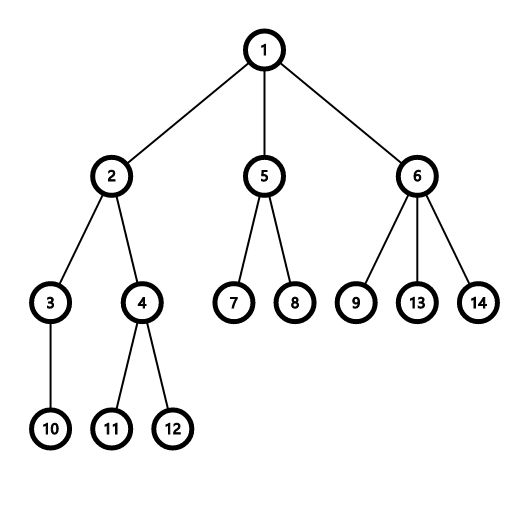
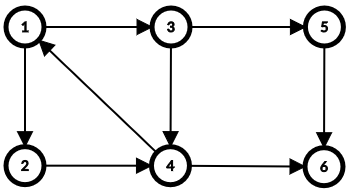
这道题我一看，按一定要求排列一个序列，这不就是我刚刚学的拓扑排序吗？

关于拓扑排序，如果不了解的，可以康一康这篇文章：【笔记】图论-拓扑排序。

思路

先用两个循环，找出所有符合题目要求的数对（比如两个数分别为aia_i和aja_j，如果ai×2=aja_i\times 2=a_j或aj×3=aia_j\times 3=a_i即为符合要求），连有向边（在上面那个例子中就是连一条从aia_i到aja_j的边），然后跑一边裸的拓扑，完事。

看上去很简单对不对？但我在写代码的时候突然想到一个问题。

拓扑排序只能处理 DAG（有向无环图），如果这个东西有环怎么办？

于是我又开始证明在这道题中按我刚才的想法建图不可能存在环，过程如下：

设uu为当前点的值，n,mn,m为任意值。

如果图中存在环，当且仅当有下面两种情况：

2n3m⋅u=12⋅u\dfrac{2^n}{3^m}\cdot u=\dfrac{1}{2}\cdot u

或

2n3m⋅u=3⋅u\dfrac{2^n}{3^m}\cdot u=3\cdot u

注：2n3m⋅u\dfrac{2^n}{3^m}\cdot u其实就是经过nn次乘22和mm次除33后所得到的值。

我们一个一个来证明。

第一种：

∵2n3m=12\because \dfrac{2^n}{3^m}=\dfrac{1}{2}

∴2n+1=3m\therefore 2^{n+1}=3^m

∵2n+1 mod 2=0,3m mod 2≠0\because 2^{n+1} \bmod 2=0,3^m \bmod 2 \not = 0

无解

第二种：

∵2n3m=3\because \dfrac{2^n}{3^m}=3

∴2n=3m+1\therefore 2^n=3^{m+1}

无解

综上所述，本题所建的图中不可能有环。

既然没有环，那我们就可以快乐地跑拓扑了！

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include<bits/stdc++.h>
using namespace std;
int n,tot,in[101],ans[101],edge[101][101];
long long a[101];
queue<int> q;
void topo()//拓扑
{
	for(int i=1;i<=n;i++)
		if(!in[i])
			q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		ans[++tot]=u;//这里我的 ans 数组是存的下标
		for(int i=1;i<=n;i++)
			if(edge[u][i])
			{
				in[i]--;
				if(!in[i])
					q.push(i);
			}
	}
	for(int i=1;i<=n;i++)
		printf("%lld ",a[ans[i]]);
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%lld",&a[i]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			if((a[i]*2==a[j])||(a[i]%3==0&&a[i]/3==a[j]))//按照上面所说的方法建图
			{
				edge[i][j]=1;
				in[j]++;
			}
	topo();
	return 0;
}

整个过程其实还是很简单的，主要是要证明没有环。