在图论中，有一类算法，是专门拿来算两点之间最短距离的，被称之为最短路算法。

一共有四种最短路算法，分别是：Floyd，Dijkstra，Bellman-Ford 和 SPFA，它们时间复杂度各不相同，同时也具有各自的缺陷，今天就来介绍一下这四种算法。

参考题目：P1744 采购特价商品（四种算法参考代码均为这道题）

PS：因为图论刚起步，所以为了熟悉一下，代码都是用的链式前向星存图，其实这四种都有自己的方式，下面会讲到。

Floyed

Floyd 和其它三种不一样，是一种全源最短路径算法，也就是说，它能求出任意点为起点，任意点为终点的最短距离，而其它三种只能求出以某一点为起点，任意点为终点的最短距离，即单源最短路径。

Floyd 算法时间复杂度为O(n3)O(n^{3})，核心代码如下：

1
2
3
4
for(int k=1;k<=n;k++)
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
            dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);

其中，k 为中间点，i 和 j 为起点和终点。

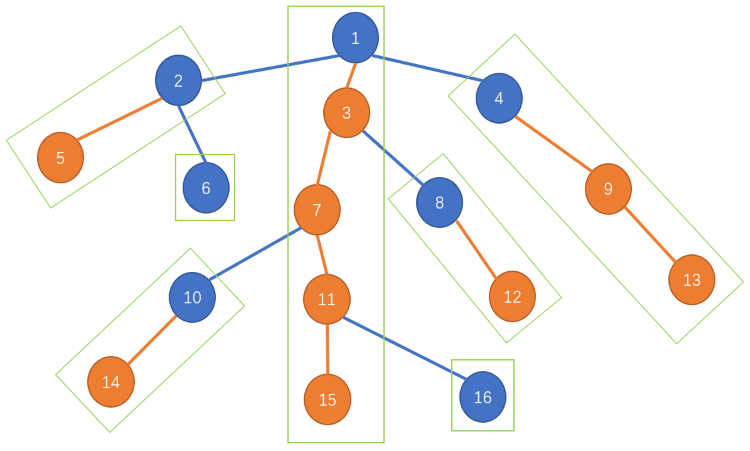
关于为什么要把 k 放在最外层，我也是纠结了很久（那肯定啊强迫症看了会很不舒服的嘛），直到看到了这张图片。

Floyed 算法

这东西把这个算法解释的很清楚了，我就不再说了。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include<cstdio>
#include<cstring>
#include<cmath>
#define min(a,b) a<b?a:b
using namespace std;
struct Point
{
	int x;
	int y;
};
Point a[101];
int n,m,s,t,cnt,h[101],b[101];
double dis[101][101];
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i].x,&a[i].y);
		for(int j=1;j<=n;j++)
			dis[i][j]=10000000;//初始化 dis 数组为无穷大，这样才能避免算的时候加入不存在的边
                               //因为是取最小值，所以这么大的数不会被考虑
	}
	scanf("%d",&m);
	for(int i=1;i<=m;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		dis[u][v]=dis[v][u]=sqrt((a[u].x-a[v].x)*(a[u].x-a[v].x)+(a[u].y-a[v].y)*(a[u].y-a[v].y));
	}
	scanf("%d%d",&s,&t);
	for(int k=1;k<=n;k++)//切记：中间点一定要放在最外层，原因上面已经讲过了
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				dis[i][j]=min(dis[i][j],dis[i][k]+dis[j][k]);//这里如果没有边，则默认为无穷大
                                                             //由于是无穷大，所以这里不可能取到不存在的边
	printf("%.2lf",dis[s][t]);
	return 0;
}

事实上 Floyd 算法并不用链式前向星，而是邻接矩阵，毕竟它是求任意点为起点和终点的最短路径，所以必须用邻接矩阵。

优点：简单易懂，全源最短路

缺点：很明显啊……时间复杂度太感人了，空间复杂度也很棒棒啊

Dijkstra

正如上面所说，Dijkstra 是一种单源最短路径算法，时间复杂度为O(n2)O(n^{2})，比较稳定。

Dijkstra 的核心思想是不停地找距离起点最近又没有更新过的点，然后对其所有相连的点进行更新。

因为从一个点到另一个点，中间必定经过至少一个中转点（把起点也算上），Dijkstra 就是不停地把距离起点最近的点作为中转点，来更新与之相连的点。

Dijkstra 默认不可能出现起点到 A 比起点到 B 距离长，但从起点经过 A 再到 B 距离却比直接到 B 短的情况，所以无法处理存在负边权的情况。

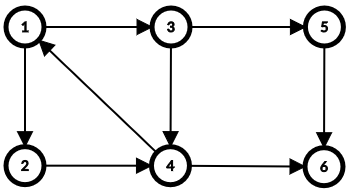
下面用图片来具体说明一下（标粗的点表示没有更新过）：

第一步：

此时，初始化dis[1]=0dis[1]=0，dis[2,3,4,5]=∞dis[2,3,4,5]=\infty，全部标记为未更新。

第二步：

此时，因为dis[1]=0dis[1]=0，距离起点最近，因此更新点 1，标记一下。然后，修改与点 1 相连的所有点，于是，dis[2]=2,dis[3]=4,dis[4]=7dis[2]=2,dis[3]=4,dis[4]=7，但这时并不标记这些点，因为它们不一定是最短路径。

数据：dis[1]=0,dis[2]=2,dis[3]=4,dis[4]=7,dis[5]=∞dis[1]=0,dis[2]=2,dis[3]=4,dis[4]=7,dis[5]=\infty

第三步：

第二轮循环后，找到点 2 距离起点最近且目前未被更新过，更新点 2，并循环与点 2 相连的所有点，即点 1，点 3，点 5，同样，这轮修改不标记，原因如上所述。因为dis[1]=0<dis[2]+2dis[1]=0<dis[2]+2，所以不修改点 1。

数据：dis[1]=0,dis[2]=2,dis[3]=3,dis[4]=7,dis[5]=4dis[1]=0,dis[2]=2,dis[3]=3,dis[4]=7,dis[5]=4

第四步：

第三轮循环，找到未被更新过的点中点 3 距起点最近，因此标记点 3，并修改与点 3 相连的点，即点 1，点 2，点 4，点 5，但因为dis[1]=0<dis[3]+4,dis[2]=2<dis[3]+1,dis[5]=4<dis[3]+6dis[1]=0<dis[3]+4,dis[2]=2<dis[3]+1,dis[5]=4<dis[3]+6，因此这三个点不管，只有点 4 被修改（同样不标记）

数据：dis[1]=0,dis[2]=2,dis[3]=3,dis[4]=4,dis[5]=4dis[1]=0,dis[2]=2,dis[3]=3,dis[4]=4,dis[5]=4

最后两轮更新将点 4 和点 5 更新，手动模拟一下发现没有点再修改了，循环结束。

综上所述，Dijkstra 算法简单来说就是，找距起点最近的点，用它来修改相连的点

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include<cstdio>
#include<cstring>
#include<cmath>
#define min(a,b) a<b?a:b
using namespace std;
struct Point
{
	int x;
	int y;
};
struct Edge
{
	int next;
	int to;
	double w;
};
Point a[101];
Edge edge[2001];
int n,m,s,t,cnt,h[101],b[101];
double dis[101];
void add_edge(int u,int v)
{
	edge[cnt].next=h[u];
	edge[cnt].to=v;
	edge[cnt].w=sqrt((a[u].x-a[v].x)*(a[u].x-a[v].x)+(a[u].y-a[v].y)*(a[u].y-a[v].y));
	h[u]=cnt;
	cnt++;
}
int main()
{
	memset(h,-1,sizeof(h));
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i].x,&a[i].y);
		dis[i]=100000000;//初始化 dis 数组无穷大
	}
	scanf("%d",&m);
	for(int i=1;i<=m;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add_edge(u,v);
		add_edge(v,u);
	}
	scanf("%d%d",&s,&t);
	dis[s]=0;//这里只初始化距离，不标记起点，否则就无法用起点去修改与之相邻的点了
	for(int i=1;i<=n;i++)
	{
		double minn=100000000;
		int mj=0;
		for(int j=1;j<=n;j++)//找距离起点最近的未更新的点
			if(b[j]==0&&dis[j]<minn)
			{
				minn=dis[j];
				mj=j;
			}
		if(mj==0)//如果没有找到，就说明要么是所有点都更新完成了，要么是没有点和起点相连
			break;
		b[mj]=1;//更新最近的点
		for(int j=h[mj];j!=-1;j=edge[j].next)//用这个点去修改相邻的点
			dis[edge[j].to]=min(dis[edge[j].to],dis[mj]+edge[j].w);//要判断一下通过这个点到达是否为最短路径
	}
	printf("%.2lf",dis[t]);
	return 0;
}

Dijkstra 算法可以用链式前向星，也可以用邻接矩阵，但个人认为链式前向星会更快一些，因为可以省去判断是否与当前点相连。

应当注意的是，Dijkstra 不能处理存在负边权的情况，如下图：

如图，从 A 到 C 最短应该是 A—>B—>C，长度为-7，但 Dijkstra 在第一轮循环的时候，就会先更新点 C 为 1，再用点 C 去修改点 B，然后更新点 B 为-9，所以无法求出最短路径。

优点：时间复杂度稳定，不容易被卡

缺点：无法处理存在负边权的情况

Bellman-Ford

Bellman-Ford 也是一种单源最短路径，其时间复杂度为O(nm)O(nm)，较 Dijkstra 来说没有那么稳定，容易被卡。

与 Dijkstra 不同，Bellman-Ford 的核心思想是，在一个图中，总有边是连接着修改过的点和未修改过的点的，通过枚举这些边，来不断修改未修改过的点的值。

具体我也不好直接说明，还是用图来手动模拟一下清晰。

PS：加粗的表示值未被修改过。

第一步：

老规矩，初始化所有点的值为无穷大，但点 1 不用，默认为 0。

数据：dis[1]=0,dis[2,3,4,5]=∞dis[1]=0,dis[2,3,4,5]=\infty

第二步：

枚举所有的边，发现dis[1]+2<dis[2],dis[1]+4<dis[3],dis[1]+7<dis[4]dis[1]+2<dis[2],dis[1]+4<dis[3],dis[1]+7<dis[4]，因此修改这些点的值dis[2]=dis[1]+2=2,dis[3]=dis[1]+4=4,dis[4]=dis[1]+7=7dis[2]=dis[1]+2=2,dis[3]=dis[1]+4=4,dis[4]=dis[1]+7=7，但在接下来的循环中，又发现dis[2]+1<dis[3]dis[2]+1<dis[3]，修改dis[3]=dis[2]+1=3dis[3]=dis[2]+1=3，dis[3]+1<dis[4]dis[3]+1<dis[4]，于是修改dis[4]=dis[3]+1=4dis[4]=dis[3]+1=4。

数据：dis[1]=0,dis[2]=2,dis[3]=3,dis[4]=4,dis[5]=∞dis[1]=0,dis[2]=2,dis[3]=3,dis[4]=4,dis[5]=\infty

第三步：

再次枚举所有的边，发现dis[2]+2<dis[5]dis[2]+2<dis[5]，于是修改dis[5]=dis[2]+2=4dis[5]=dis[2]+2=4，而后又发现dis[3]+6>dis[5]dis[3]+6>dis[5]，于是dis[5]dis[5]修改完毕，至此，所有的点都修改完了。

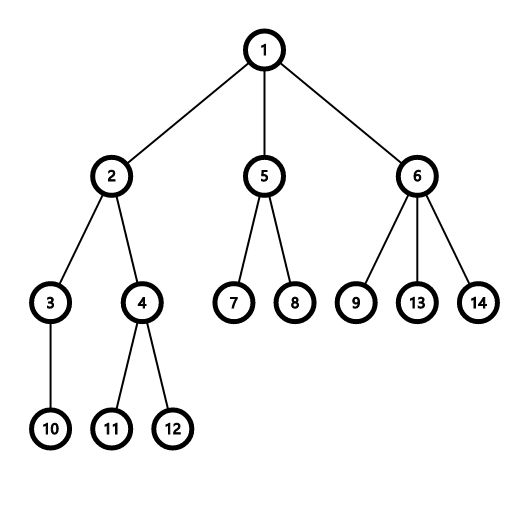
关于为什么 Bellman-Ford 要循环nn次，其实很简单，虽然上面这个图只用了 3 次就完成了，但不能排除有链的情况，比如这样：

这时，每次循环所有边就只能改变一个点的值，所以至少要循环 5 次。

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include<cstdio>
#include<cstring>
#include<cmath>
#define min(a,b) a<b?a:b
using namespace std;
struct Point
{
	int x;
	int y;
};
struct Edge
{
	int next;
	int to;
	double w;
};
Point a[101];
Edge edge[2001];
int n,m,s,t,cnt,h[101];
double dis[101];
void add_edge(int u,int v)
{
	edge[cnt].next=h[u];
	edge[cnt].to=v;
	edge[cnt].w=sqrt((a[u].x-a[v].x)*(a[u].x-a[v].x)+(a[u].y-a[v].y)*(a[u].y-a[v].y));
	h[u]=cnt;
	cnt++;
}
int main()
{
	memset(h,-1,sizeof(h));
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i].x,&a[i].y);
		dis[i]=100000000;
	}
	scanf("%d",&m);
	for(int i=1;i<=m;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add_edge(u,v);
		add_edge(v,u);
	}
	scanf("%d%d",&s,&t);
	dis[s]=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)//链式前向星遍历所有边
                             //其实也可以用一个 f[2*m][2] 的数组来存每条边的起点与终点，会更方便
                             //之所以是 2*m，是因为这是无向图，每条边要存两次
			for(int k=h[j];k!=-1;k=edge[k].next)
				dis[edge[k].to]=min(dis[j]+edge[k].w,dis[edge[k].to]);//判断通过当前这条边到达这个点会不会更短
	printf("%.2lf",dis[t]);
	return 0;
}

Bellman-Ford 可以不用链式前向星，而直接单纯地存边的起讫点，在时间上区别个人认为不大，但空间的话还是后者要优秀一点。

Bellman-Ford 无法处理存在负权回路的情况，即这条回路上所有边的权值加起来为负数的回路（废话这样一直转下去每次减一点值就无穷小了呀），就像这样：

尽管 Bellman-Ford 无法处理负权回路的情况，但可以判断是否存在负权回路，如果全部循环完了，还存在某条边使得从点 A 到点 B 的距离更小，就存在负权回路。

直接在两重循环完了后面加上这样几行代码即可：

1
2
3
4
for(int i=1;i<=n;i++)
    for(int j=head[i];j!=-1;j=edge[j].next)//链式前向星遍历
        if(dis[edge[j].to]>dis[i]+edge[j].w)
            printf("啊啊啊有负权回路啊！！！");

优点：可以处理负边权的情况，可以检测负权回路

缺点：容易被卡！！！

SPFA

SPFA 是 Bellman-Ford 的队列优化版本，时间复杂度和 Bellman-Ford 一样，是O(nm)O(nm)（不要信《信息学奥赛一本通》上的鬼话，它说时间复杂度是 O(km)，其中 k 是常数，约为 2，根本不对，详见 [百度](https://baike.baidu.com/item/SPFA 算法/8297411?fromtitle=SPFA&fromid=11018124&fr=aladdin)）

SPFA 的思路非常简单，每次从队头取一个点出来，判断从这个点到相邻的点是否更短，如果是，则将这个相邻的点入队，其实就和 BFS 很像，但不同的是，SPFA 中的点可以多次入队，因为第一次找到的最短路径不一定就是真正的最短路径。同时，也正因为可以多次入队，所以它无法像普通的 BFS 一样估算队列的长度，所以在实现时，要么采用循环队列（即把队列当成一个圆环，当队尾到达一定位置时，就把尾指针移到队头，相当于从头再开始存，一般是用一个取模来完成，这样比较方便），这时队列只需开到2∗n+52*n+5即可（《信息学奥赛一本通》原话，具体证明我也不会，如果哪位大佬知道的话麻烦在评论里指出，蟹蟹！），要么还可以用 STL 库中的 queue 容器，这里我用的是 queue，但也要学会手打队列，不能养成 STL 依赖症。

参考代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
#include<cstdio>
#include<cmath>
#include<queue>
#define min(a,b) a<b?a:b
using namespace std;
struct Point
{
	int x;
	int y;
};
struct Edge
{
	int next;
	int to;
	double w;
};
Point a[101];
Edge edge[2001];
int n,m,s,t,cnt,head[101];
double dis[101];
queue<int> q;
void add_edge(int u,int v)
{
	edge[cnt].next=head[u];
	edge[cnt].to=v;
	edge[cnt].w=sqrt((a[u].x-a[v].x)*(a[u].x-a[v].x)+(a[u].y-a[v].y)*(a[u].y-a[v].y));
	head[u]=cnt;
	cnt++;
}
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",&a[i].x,&a[i].y);
		dis[i]=10000000;
		head[i]=-1;
	}
	scanf("%d",&m);
	for(int i=1;i<=m;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		add_edge(u,v);
		add_edge(v,u);
	}
	scanf("%d%d",&s,&t);
	q.push(s);//一开始起点入队
	dis[s]=0;
	while(!q.empty())
	{
		for(int i=head[q.front()];i!=-1;i=edge[i].next)
			if(dis[q.front()]+edge[i].w<dis[edge[i].to])//判断相邻的点通过当前点到达是否更短
			{
				dis[edge[i].to]=dis[q.front()]+edge[i].w;
				q.push(edge[i].to);//如果是，则当前点的值修改，并入队
			}
		q.pop();
	}
	printf("%.2lf",dis[t]);
	return 0;
}

整个过程其实和 BFS 几乎完全一样，这里我介绍一下 queue 容器的使用。

使用 queue 容器要包含#include<queue>这个头文件。

queue 的定义格式是queue<元素类型>队列名称，如：queue<int>qwq就是定义了一个名字为 qwq，元素类型为 int 的队列

queue 一共有 6 个常用函数：

  1. qwq.push(x)：将 x 元素入队

  2. qwq.pop()：将队头元素出队

  3. qwq.front()：返回队头元素的值（但不出队）

  4. qwq.back()：返回队尾元素的值（个人觉得用处不大）

  5. qwq.empty()：判断队列是否为空，如果为空，则返回true

  6. qwq.size()：返回队列中元素个数

差不多就是这些了，如果还有什么，我后面再补充。

特别注意：SPFA 容易被卡！

在此放上一张经久不衰的图片：

2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 里非常熟练地使用了一个广为人知的算法 SPFA 求最短路。

然后呢？

100→60100 \rightarrow 60；

Ag→CuAg \rightarrow Cu；

最终，他因此没能与理想的大学达成契约。

由于 SPFA“优秀”的时间复杂度，所以它经常在各大 OJ 和 OI 上被卡，再引用一个人的话。

卡 SPFA 已经是一个共识了好吧……

所以在比赛时，最好还是不要用 SPFA 了……

优点：比较简单易懂，而且可以处理负边权的情况

缺点：容易被卡

总结

四种最短路径算法个人觉得还是根据具体的题目来看吧，但一般来说我觉得应该是没有负边权就用 Dijkstra（实在不行加个堆优化），有负边权就用 SPFA 好了，也没有必要一味地说 SPFA 死了，毕竟既然这玩意还没有完全被淘汰不用，就说明它还是有自己的用途的。